Cognitive Load Theory: Research that teachers really need to understand
- Dan Rodriguez-Clark
- Sep 25, 2017
- 5 min read
Author: Centre for Education Statistics an Evaluation, NSW Department of Education
Article: Story of a Research Program
Author: John Sweller
"I've come to the conclusion Sweller's Cognitive Load Theory is the single most important thing for teachers to know" - Dylan Wiliam, 2017, https://twitter.com/dylanwiliam/status/824682504602943489
The former of the two articles is a brief summary of the research into cognitive load theory and what it is, followed by an overview of the most important aspects for teachers to consider in designing learning sequences. The latter article is written by John Sweller, the man who came up with cognitive load theory, and in it he gives his personal journey through the research, which started in the 1980s and is still ongoing. It covers a bit more of the details of the theory.
I will try to distil the information in as succinct a way as possible, but, at 7 pages, the report from CESE is an essential read for all teachers.
My understanding of Cognitive Load Theory
In previous posts I have discussed the model of the mind which incorporates the working memory and the long term memory. Working memory is "the memory system where small amounts of information are stored for a very short duration" (CESE, 2017) and is easily thought of as the information that we are currently conscious of. This is limited to approximately 4 units. On the other hand, long term memory is "the memory system where large amounts of information are stored semi-permanently" (CESE, 2017) and can be considered as the storage of things we have previously learned. For all intents and purposes, this is unlimited in size.
Long term memory is made up of schemas, which, roughly speaking, connect the interlinked parts of what we know. Schemas can become very complex, and they build upon each other when two or more simple schemas combine to form a more complex schema. The important part of schemas is that they only take up a single element of working memory, so "a high level schema - with potentially infinite informational complexity - can effectively bypass the limits of working memory" (CESE, 2017).

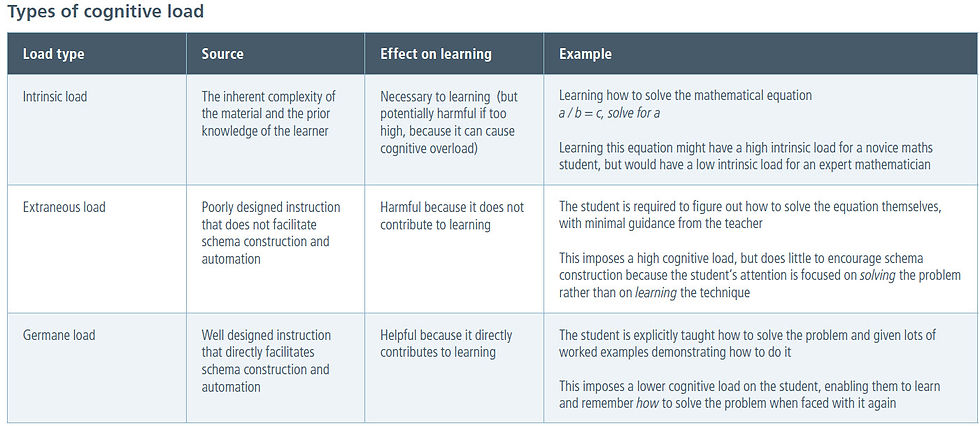
Cognitive load theory asserts that the working memory is limited, and that when too much information is trying to be stored or processed we experience cognitive overload. There are three types of cognitive load (types of information that can take up working memory) which are:
Intrinsic cognitive load - which is directly related to the relative difficulty of the task at hand. How much load this causes depends on the complexity of the material and the prior knowledge of the individual. This can be thought of as the "necessary" cognitive load.
Extraneous cognitive load - which is load caused by things not related to the learning. This includes any process which takes up working memory in the learning process. This can be thought of as the "bad" cognitive load.
Germane cognitive load - which is the load caused by the process of learning. This is obviously the "good" type of cognitive load.
These three types are additive, so that if one is using a unit of cognitive load, it cannot be used for something else. If too much intrinsic and extraneous load are used during instruction, then students do not have enough space for the germane load to function and thus for them to learn the material. That is, as teachers, we need to ensure at any stage students have enough working memory free to process the information and save it to long term memory. If this space is not available, students will not learn anything.
John Sweller (2016) gives a very good example of this from one of his earliest studies. Undergraduate students were asked to get from one number to another by using only two moves: multiply by 3 or subtract 29. For example to get from 16 to 19 you first multiply 16 by 3 to get 48, then subtract 29 to get 19. All students solved the problems, but very few noticed the underlying structure of all the problems: they all followed the pattern of alternating multiply by 3 then subtract 29 in that order. The students were using all their working memory on solving the problems, leaving no space left for them to "learn" the pattern (Sweller, Mawer and Howe, 1982). Although very simple, this has since been shown through many more in depth studies.
The further research into cognitive load theory has found many effects that have direct implications on our classroom practice. CESE (2017) identifies 5 of these effects (effects 2, 3, 4, 5 and 6 in the image below) as being particularly important for instructional design, whilst Sweller (2016) discusses a further 9, as well as covering the original 5 in more depth. The image below is from Oliver Caviglioli, based on John Sweller's full book, Cognitive Load Theory.

Image - Oliver Caviglioli (@olivercavigliol)
My reflection
I have been learning about cognitive load theory over the last few months, and I am just starting to get to a position where I think I understand the basics fairly well. I have already been implementing the worked example effect in my classroom. I have started to focus on reducing both intrinsic and extraneous cognitive load as well.
To reduce intrinsic cognitive load I am focusing on breaking up the material into small steps, which the CESE describes as "the 'part-whole' approach, where the individual elements of the material are introduced to the learner first, before the integrated task is introduced". This has been working well as far as I can tell in the immediate feedback stage, but we will see if this has actually helped improve the long term memory of the students.
I have also attempted to reduce extraneous cognitive load in three main ways. The first is to remove unnecessary animations and distractions from my slides, which is to do with the redundancy effect. The second is to get students to read material from the board rather than read it out (the redundancy effect again). The third is to stop using discovery learning in the initial stages of instruction (which I have talked about before here).
I do need to be careful with this though, as the expertise reversal effect suggests that as we approach the end of a particular unit, and students are becoming relative "experts" in that topic, I should be building in more opportunities for independent problem solving.
I have also not been focusing on the split-attention effect or the modality effect. The split-attention effect could be causing problems in geometry problems, so I need to reconsider how I lay out the diagrams for questions and examples.
Although I am starting to get to grips with the ideas of cognitive load theory, I am certainly far from becoming an expert in them, and over the next few months I am going to continue to actively try to incorporate the ideas into my teaching, along with those on performance vs learning that I have previously written about.
References
Centre for Education Statistics and Evaluation 2017, Cognitive load theory: Research that teachers really need to understand.
Sweller, J 2016, "Story of a research program", Education Review, vol. 23, p.1-18.
Sweller, J, Mawer, R and Howe, W 1982, "Consequences of history-cued and means-end strategies in problem solving", American Journal of Psychology, vol. 95, pp. 455-483.
Comments