Variation Theory in Maths
- Rodrigo Rivadeneira
- Jun 11, 2018
- 4 min read
Variation theory is a concept which I heard from Dan a few weeks ago.
When practicing a particular skill in a repetitive way we as teachers tend to think about the increasing level of difficulty from one set of exercises to the next. For example, if we are practicing solving linear equations we might start with those which can be solved in one step, then practice ones which can be solved with two steps, then three steps and so on. In the past I used to think these filtres were good enough to scaffold the repetitive exercising students must go through. However, there are smaller changes in each exercise that can make a difference between just repetition and developing understanding.
Repetitive exercises are usually linked to developing a mechanic, a procedure to work out a problem rather than understanding. If too much is changed from one exercise to the next, then that is probably what will happen. However, if only one aspect of an exercise is changed and everything else remains the same, then a student can focus on what has changed and begin to develop an understanding of how that single change affects the rest of the problem. This is called, apparently, variation theory and today I used in an unconventional way.
I was teaching straight line graphs to S2 students. We were going to look at how to find the equation of a straight line when they are given the straight line graph and some information. We had already looked at how to do this using squared paper. Students already know that they need to find the gradient of the line and the y-intercept. This is pretty easy using squared paper. Students count squares to find the gradient (the hard part) and then they just identify the point where the line cuts the y-axis (the easy part). This can be seen in the picture below.
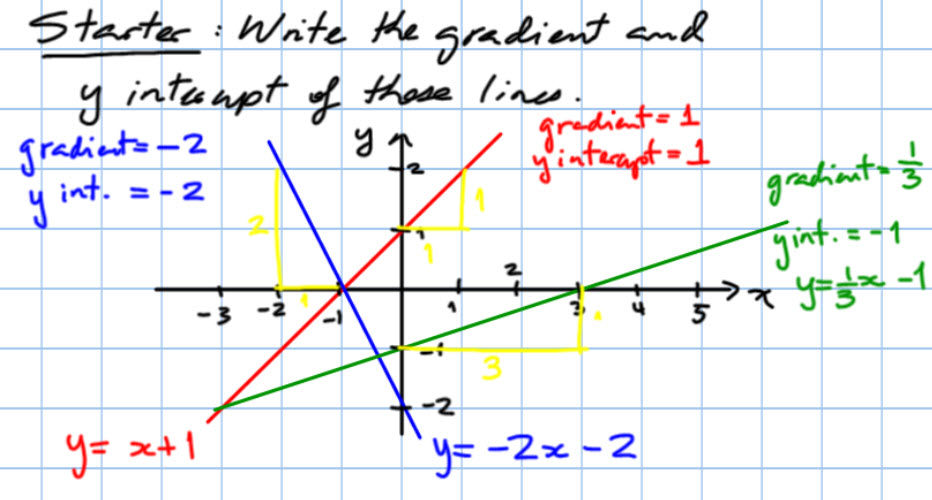
The yellow triangles constructed underneath the straight lines in red, blue and green show how squares are counted to find the gradient of the line. This is an easy process with squared paper.
In real IGCSE examinations, students will not usually have such a information-filled diagram. They will most likely have to work with a diagram not to scale and without a squared grid to help them. In this case, counting squares to fill in the yellow triangles is not possible, so they need a different strategy. They are meant to use fixed points on the diagram to find vertical and horizontal differences, or at least that what we want to do eventually. So I showed them the same example, with all the working out already done, but without the squared paper, as shown in the diagram below.
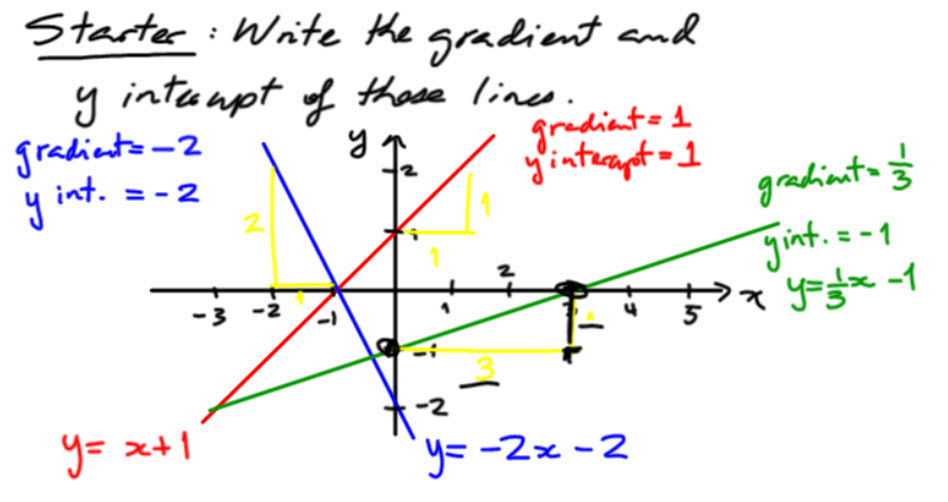
Nothing else has changed, only the squared paper background. The students can now focus on how that single change affects everything else.
T: “Would you be able to work everything out again in the same way without the squared background?”
I ask them this and immediately students start to yell out yes or no, but some dayled answers show evidence of deeper consideration.
S1: “The yellow triangles cannot be done without the grid”
S2: “The one under the green line can, you don’t need squares for that one”
It took a little bit of time, but someone got it and then other got it, and then everyone got it. The yellow triangles can be done, but they need to be done using fixed point already given in the diagram, as shown below.
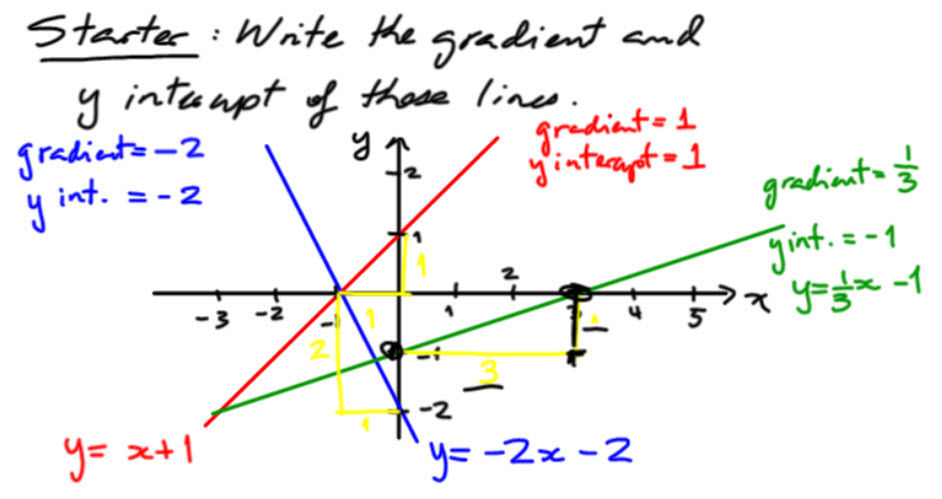
I only changed one thing, and it was not even a mathematical thing. I took away the squared background and asked a question. The rest snowballed from there and students had a chance to focus on how one single factor affects the strategy to solve a problem.
What would have happened if I had used a completely different set of lines? What would students be focusing on with that new change? What questions would arise and how relevant would they be?
“Sir, but the gradient is now negative and not positive…how do we write the equation now?”
This sounds like a possible question that might arise if I had used a completely new set of line. It even sounds very relevant to the topic we are looking at and is a completely valid question. However, it is not the most relevant if I want them to focus only on how to find gradients without squared paper. It would have been a dangerous question, because it is so good in terms of the general topic, that it could have even pulled other students attention to it. I do not want to be in a position where a student has a good question but I have to dismiss it because it is drifting away from the main focus (again).
After the example, it was clear to me at that point that the majority (if not all of them) understood why the yellow triangles needed to be formed using fixed points when squared paper is not available or the diagram is not to scale. On to exercises and making sure everyone got it in practice.
Comments